Бо мо дарси аввалини геометрияи таҳлилӣ дарс омӯзед! Риёзӣ 2 ва Ҳисобон 1-ро бо тарзи фаҳмо ва осон омӯзиш диҳем. Дар ин видео, мо ба шумо тартиби асосии геометрияи таҳлилӣ ва формулаҳои муҳимеро, ки ба шумо дар фаҳмидани мавзӯъ кӯмак мерасонанд, нишон медиҳем. Барои ҳалли масъалаҳои мураккабтар бо мо бимонед! Ҳамаи чизҳое, ки барои муваффақ шудан дар имтиҳонҳо лозим аст, дар инҷост.

Дар ин видео, мо ба шумо як дарси пурраи геометрияи аналитикӣ ва ҳисоббарории 1, ки барои синфи ёздаҳуми мактаб аст, пешниҳод мекунем. Бо мо ҳамроҳ бошед, то фаҳмиши комил ва қадам ба қадам аз мавзӯъҳои муҳимро дастрас кунед. Ин видеои омӯзишӣ барои донишомӯзоне, ки мехоҳанд дарсҳои геометрияи аналитикӣ ва ҳисоббарориро ба таври амиқ фаҳманд, хеле муфид аст.

Мо дар ин видео дарси панҷум аз фасли аввал китоби ҳисобиёти синфи ёздаҳумро баррасӣ мекунем. Геометрияи таҳлилӣ мавзӯи асосии ин дарс аст ва мо кӯшиш мекунем, ки онро бо роҳи содда ва фаҳмо фаҳмонем. Агар мехоҳед, ки ба ҳисобиёти худ беҳтар фаҳмед, ин видео барои шумост!

Дар ин видео, мо ба дарси 4 аз фасли якуми ҳисобиёт 1 мегузарем ва ба мавзӯи геометрияи таҳлилӣ диққат медиҳем. Биёед бо ҳамроҳӣ ин мавзӯъи ҷолибро омӯзем ва аз ҳисобиёт лаззат барем!

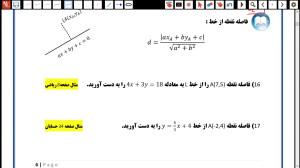
Дар ин видео, мо ба шумо нишон медиҳем, ки чӣ тавр масофаи байни нуқта ва хатро дар геометрияи аналитикӣ ҳисоб кунем. Қисми сеюм аз ин силсила, бо мисолҳои равшан ва тавзеҳоти осон, шумо метавонед зуд ин мафҳумҳоро фаҳмед ва дар амал татбиқ кунед. Биёед якҷоя омӯзем ва барномаи худро васеъ кунем!

Дар ин видео мо ба дарси понздаҳуми силсилаи омӯзиши геометрияи алгебравии функсионалӣ ворид мешавем. Агар мехоҳед дар бораи назарияи алгебра ва функсионалӣ маълумоти бештар гиред, ин видео барои шумост. Дарсҳо бо мисолҳои воқеӣ ва тавзеҳоти оддӣ пешниҳод мешаванд, ки фаҳмиданро осон мекунанд. Ҳатман обуна шавед ва ба дигарон низ тавсия диҳед!

Дар ин видео мо ба машқҳои саҳифаи 48 фасли 3 геометрияи синфи нӯҳум назар мекунем. Бо усулҳои осону равшан, шумо метавонед ин машқҳоро ҳал кунед ва маҳоратҳои геометрияи худро такмил диҳед. Тамошо кунед ва аз имкониятҳо истифода баред, то ба саволҳо ҷавоб диҳед ва дарсҳоро беҳтар фаҳмед.

Ҳамаи ҷавобҳои дурусти имтиҳони фасли якуми геометрияи синфи даҳумро кашф кунед! Ин видео барои шогирдоне, ки мехоҳанд ба осонӣ ва самаранок дарс тайёр кунанд, кӯмак мекунад. Бо мо бошед, то ба муваффақият бирасед!

Бо мо дарсҳои геометрияи аналитикиро омӯзед ва фаҳмиши математикаро баланд бардоред! Дарсҳои шавқовар ва фаҳмову осон барои ҳама синфҳо. Аз ҳоло оғоз кунед ва аз ҳамроҳии мо баҳра баред!

Дар ин видеои супертамошобоб, мо ба қисми сеюми геометрияи синфи 12 барои шӯъбаҳои математика ва физика мепардозем. Ба шумо фаҳмиши амиқ ва роҳҳои осон барои ҳал кардани масъалаҳои мураккабро пешкаш мекунем. Тайёр бошед, ки бо мо ба ҷаҳони геометрияи ҷолиб ворид шавед!

Бо мо дар ин видео масофаи ду нуқтаро дар геометрияи аналитикӣ омӯзед! Мо тамоми формулаҳо ва қадамҳоро барои ҳисоби ин масъала дарс медиҳем. Барои донишҷӯёни синфи 11, ин қисми 2 аз силсилаи видеоҳои мо дар бораи алгебра ва ҳисоби аст. Ҳамаи нуктаҳои муҳимро ёд гиред ва ба саволҳои худ посух ёбед.

Дар дарси шонздаҳуми ин силсила, ба мавзӯи ҷолиби геометрияи алгебравии функториалӣ шинос мешавем. Агар мехоҳед дар бораи ин мавзӯи муҳим маълумоти бештар гиред, ин видеоро тамошо кунед!

Ин видеои чордаҳум аз силсилаи дарсҳо дар бораи геометрияи алҷабрии функсионалӣ аст. Бо мо шинос шавед ва дар бораи асосҳои ин мавзӯи ҷолиб маълумоти бештар гиред. Дар ин дарс мо ба ҷанбаҳои ҷолиб ва татбиқоти гуногуни геометрияи алҷабрии функсионалӣ нигоҳ мекунем.

Дар ин видео мо бо як забони содда ва равшан бурҳони халафро аз китоби геометрияи синфи даҳум меомӯзем. Агар дар бурҳони халаф мушкилӣ доред, ин видео барои шумо аст! Биёед якҷо ин мавзӯъро омӯзем ва ба саволҳоятон ҷавоб ёбем.

Дар ин видео, ба шумо дарси аввалини фасли риёзӣ 2 - геометрияи таҳлилӣ ва алгебраро пешниҳод мекунем. Омӯзиши ин мавзӯъҳо барои ҳар касе, ки мехоҳад дар риёзӣ муваффақ шавад, муҳим аст. Ба мо ҳамроҳ шавед ва донишҳои худро такмил диҳед!

Мехоҳед ба таҳлили пурраи имтиҳони марҳилаи сеюми геометрияи синфи 10 бо устод Воъизин шинос шавед? Дар ин видео мо ҳама чизеро, ки барои омодагӣ ба ин имтиҳон ниёз доред, баррасӣ мекунем. Аз маслиҳатҳо ва стратегияҳои муваффақият то таҳлили саволҳои мушкил, ба ҳама чиз расида мепардозем. Агар шумо хоҳед, ки дар имтиҳонҳои оянда натиҷаҳои беҳтарин ба даст оред, ин видео барои шумост!

Дар ин видео мо ба таҳлили геометрияи имтиҳонҳои мактабҳои беҳтарин пардохтаем. Барои онҳое, ки мехоҳанд дар имтиҳонҳо муваффақ шаванд ва аз мактабҳои номдор қабул шаванд, ин видео ба шумо кӯмак мекунад, ки тақрибан ҳама чизро омӯхта, беҳтарин натиҷаҳоро ба даст оред. Агар шумо ҳам мехоҳед, ки дар имтиҳонҳои мактабҳои олӣ бартарӣ ба даст оред, ин видеоро тамошо кунед ва аз маслиҳатҳои мо истифода баред.

Дар ин видео, мо таҳлили пурраи имтиҳони марҳилаи дуюми геометрияи синфи 10-ро бо устод Воизин пешниҳод мекунем. Агар мехоҳед дар ин имтиҳон муваффақ шавед, ин видео барои шумо ҳатмист. Биёед бо усулҳои нав ва маслиҳатҳои устод Воизин омодагии худро ба сатҳи нав бардорем.

Дар ин видео мо ба таҳлили пурраи имтиҳони геометрияи синфи 12 аз Қалами Чӣ, ки 17-уми ноябри 2024 баргузор шуд, машғул мешавем. Барои онҳое, ки мехоҳанд ба имтиҳонҳои худ тайёр шаванд ва ба беҳтарин натиҷаҳо даст ёбанд, ин видео як захираи гаронбаҳо хоҳад буд. Шумо метавонед аз машқҳо ва маслиҳатҳои мо истифода баред ва омодагии худро баланд бардоред. Дарси мо ба шумо кӯмак мекунад, ки ҳама ҷанбаҳои муҳими имтиҳонро дарк кунед ва ба саволҳои имтиҳонӣ бо эътимод ҷавоб диҳед.

Дар ин видео мо ба таҳлили пурраи имтиҳони марҳилаи дуюми риёзиёти дискретӣ ва геометрияи синфи 12 бо устоди моҳир Доробӣ мепардозем. Агар шумо мехоҳед ки ба имтиҳонҳои оянда омодагии комил дошта бошед ва холҳои баланд ба даст оред, ин видео барои шумост! Устод Доробӣ маслиҳатҳои нодир ва тавсияҳои муфид медиҳад, ки ба шумо дар фаҳмиши беҳтари мавзӯъҳо кӯмак мекунад. Биёед якҷоя ин имтиҳонро таҳлил кунем ва ба муваффақият қадам гузорем!