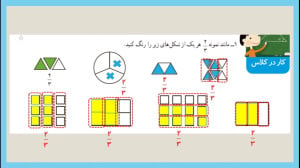
Салом ба ҳама! Дар ин видео мо фасли чорум аз математикаи синфи ҳаштумро омӯхта, бо ҳама масъалаҳо ва қоидаҳо шинос мешавем. Ин видео барои касоне, ки мехоҳанд математикаи синфи ҳаштумро беҳтар дарк кунанд, хеле муфид аст. Ҳамроҳ шавед, то ҳама чизро хуб фаҳмед!
Дар ин видео, мо ба дарси чорум аз фасли чорум риёзии синфи нуҳум назар мекунем. Ин дарс барои шогирдон муҳим аст, ки мехоҳанд дар риёзӣ муваффақ шаванд ва бофтаҳои навро омӯзанд. Ҳамроҳ шавед ва ҳама чизро дар бораи ин мавзӯъ фаҳмед!
Дар ин видео мо ба дарси чорум аз синфи чорум сар мекунем, ки арзиши илму донишро меомӯзад. Саҳифаҳои 25 то 30 пур аз маълумоти ҷолибанд, ки ба шумо кӯмак мекунад, ки донишатонро афзоиш диҳед. Биёед якҷоя худшиносӣ кунем ва фаҳмем, ки чаро илму дониш ин қадар муҳим аст!
Дар ин видео мо ба дарси чорум аз омӯзиши иҷтимоии синфи чорум таваҷҷӯҳ мекунем. Бо мо ҳамроҳ шавед, то фаҳмишҳои навро дар бораи мавзӯъҳои иҷтимоӣ касб кунед. Агар мехоҳед дар бораи ҷомеаи мо бештар бидонед, ин дарсро тамошо кунед!
Кисми чорум фасли чорум LCDL-ро тамошо кунед! Дар ин қисм, мо ба ҳодисаҳое, ки шуморо дар ҳайрат мегузоранд, ворид мешавем ва қиссаҳоеро, ки пешгӯйии онҳоро душвор аст, мекушоем. Ҳаргиз ин қисматро аз даст надиҳед!
Мехоҳед саҳифаҳои 34, 35 ва 36 аз китоби математикаи синфи чорумро бе мушкил ҳал кунед? Видеои моро тамошо кунед, то ҳама қадамҳоро бо осонӣ ва шеваи равшан бифаҳмед! Ин видео барои толибилмон ва волидон, ки мехоҳанд ба фарзандонашон дар омӯхтани математика кӯмак кунанд, ки хеле муфид аст!
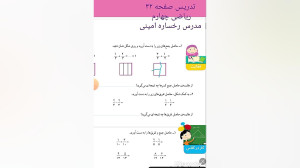
Дар ин видео мо якҷоя бо муаллимаи олиҷаноб Рахсора Амини саҳифаи 32-и китоби математикаи синфи чорумро омӯхта мебароем. Ба мо ҳамроҳ шавед, то бо усулҳои нав ва шавқовари таълимӣ шинос шавед ва донишатонро қавӣ кунед. Агар масъалае дошта бошед ё саволе пайдо шавад, дар шарҳҳо нависед, ва мо ба шумо кӯмак мекунем!
Салом ба ҳама! Дар ин видео мо ба шарҳ ва ҳалли намунаи саволҳои фасли аввал математикаи синфи чорум мепардозем. Агар шумо хоҳед, ки дарсҳоро бо шавқу завқ омӯзед ва дар имтиҳонҳо комёб шавед, пас ин видео барои шумост. Ҳар саволро бо тафсил шарҳ медиҳем ва роҳҳои осонтарини ҳалли онҳоро нишон медиҳем. Дар канали мо обуна шавед, то аз навигариҳои мо бохабар бошед!
Дар ин видео мо саҳифаи 60 аз китоби математикаи синфи чорумро бо шарҳҳои пурра меомӯзем. Ҳар як қадамро равшан ва фаҳмо шарҳ медиҳем, то шумо бе мушкилӣ дарк кунед. Ҳар як мушкилотро бо роҳҳалҳои оддӣ ва самаранок ҳал мекунем. Вақти худро сарфа кунед ва бо мо ба ҳалли масъалаҳои математикаи синфи чорум шавқманд гардед!
Омӯзиши пурра ва пурмазмуни математикаи синфи чорум дар саҳифаи 19 аз китоби мактаби ибтидоӣ. Ин видео барои кӯмак ба хонандагон дар фаҳмидани мавзӯъҳои муҳим ва вусъати дониши онҳо таҳия шудааст. Агар шумо мехоҳед ба математикаи худ боварӣ ҳосил кунед, ин видеоро тамошо кунед!
Ҳалли пурраи масоили математикаи синфи чорум саҳифаҳои 20 ва 21. Хубтарини роҳи ҳалли масъалаҳоро омӯзед ва дарсҳои худро бо осонӣ фаҳмед. Ҳамаи қадамҳоро пайравӣ кунед ва суръати худро дар математика баланд бардоред!
Дар ин видео, мо ба шумо дарси чорум аз математикаи синфи ҳаштро ба таври осон ва фаҳмо мефаҳмонем. Қисми сеюми ин дарсро тамошо кунед, то ки беҳтар фаҳмед ва дарсҳои мушкилро осонтар кунед. Агар шумо бо математика мушкилӣ дошта бошед, пас ин видео барои шумо аст! Ба канали мо обуна шавед, то ки дигар дарсҳои муфидро аз даст надиҳед.
Дар ин видео, мо ба фасли чорум дар фанҳо барои синфи чорум сар мекунем. Дарс дар бораи ҳаракат ва қувваҳо дар табиат аст. Бо мо бошед, то ки бо осонӣ ва шавқомез ин мавзӯъро омӯзед!
Дар ин видео мо ба шумо омӯзиши геоэлектрикии обёбии замини бехатарро нишон медиҳем. Қисми чорум аз фасли чорум, ки дар бораи техникаҳои муосир ва бехатар барои обёбии заминҳои шумо маълумот медиҳад. Барои маълумоти бештар ва ёфтан роҳи беҳтарин, ин видео тамошо кунед!
Дар ин видео, мо ба асосҳои ҳисобкунии математикаи дискретӣ назар мекунем. Ин мавзӯъ барои ҳамае, ки мехоҳанд дар соҳаи илмҳои компютерӣ ва математикаи пешрафта пешравӣ кунанд, муҳим аст. Барномаро тамошо кунед ва фаҳмишатонро васеъ кунед!
Ҳамаи чизҳое, ки шумо бояд дар бораи математикаи дискретӣ донед! Дар ин видео мо ба шумо назаре гузаронида, ба мавзӯъҳои муҳим ва насибҳоҳои асосии математикаи дискретӣ мепардозем. Аз ин фурсати нодир истифода баред ва ба донишҳои худ афзун кунед!
Дӯстони азиз! Дар ин видео мо саҳифаи 26 аз китоби математикаи синфи 9-ро бо ҳам таҳлил мекунем. Фасли 2 ба ададҳои ҳақиқӣ бахшида шудааст. Агар дар ин мавзӯъ саволе дошта бошед, ҳатман дар шарҳҳо бинависед. Омодагӣ ба имтиҳонҳоро бо мо осон кунед!
Ба саҳифаи 46-и китобҳои математикаи синфи 7 ғарқ мешавем! Ин видео ба шумо тамоми ҷузъиёти фасли 4-ро нишон медиҳад. Агар мехоҳед дар дарсҳои математикаи худ беҳтар шавед, ин видеоро то охир тамошо кунед!