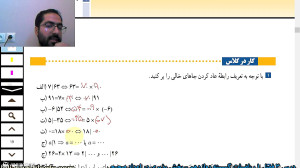
Ҳалномаи масъалаҳои саҳифаи 19 аз китоби математикаи синфи 7-ро чӣ тавр фаҳмидан мумкин аст? Мо бо усулҳои осон ва фаҳмо ба шумо кӯмак мекунем, то дарсҳои математикаи худро беҳтар фаҳмед. Дар ин видео, мо ба шумо ҳар қадамро нишон медиҳем. Аз даст надиҳед!

Ҳалномаи пурра барои саволҳои математикаи синфи 7 дар саҳифаи 18. Ба шумо нишон медиҳем, ки чӣ тавр ин масъалаҳоро осон ҳал кунед ва ба дарки пурра расед. Аз ин видео боҳаловат шавед ва бо мо дар роҳи омӯзиш қадам ба қадам пеш равед.

Ҳалномаи пурраи мисолҳои саҳифаи 10 аз китоби риёзиёти дискретии синфи 12. Ба мо ҳамроҳ шавед, то бо усулҳои нав ва фаҳмиши амиқ мисолҳои ин саҳифаро ҳал кунем. Ҳамроҳ бошед ва ба дониши худ илова кунед!

Ҳалномаи пурра ва машқҳои саҳифаи 48 аз китоби математикаи синфи шашум бо роҳнамоии Боқерӣ Фард. Биёед дарси худро бо усулҳои осон ва фаҳмову равшан ёд гирем ва баҳсҳоро бо ҳамдигар ҳал кунем. Ин видео барои онҳое, ки мехоҳанд ба осонӣ ва зуд дарсҳои математикаи худро ба итмом расонанд, хеле муфид аст.

Ҳалномаи пурраи саҳифаи 38 аз китоби математикаи синфи сеюмро дар ин видео пайдо кунед! Бо тавзеҳоти оддӣ ва фаҳмо, ҳамаи саволҳо ва мисолҳоро қадам ба қадам ҳал мекунем. Барои фаҳмиши беҳтар ва омодагии пурра барои имтиҳонҳо моро тамошо кунед!

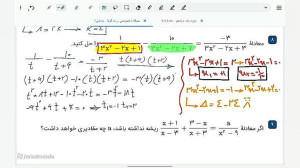
Ҳалномаи муодилаҳои бисёрҷумлаӣ дар қисми дуюм! Мо ба шумо роҳи осони фаҳмишро нишон медиҳем. Барои фаҳмидани чӣ тавр муодилаҳои мураккабро ҳал кардан, тамошо кунед ва дарсҳои навро аз даст надиҳед!

Ҳалномаи машқҳои саҳифаи 58 аз китоби риёзии синфи 7. Дар ин видео, мо якҷоя машқҳоро ҳал мекунем ва ба шумо роҳи дурусти коркарди масъалаҳоро нишон медиҳем. Барои беҳтар фаҳмидани математика, ба мо ҳамроҳ шавед!

Ҳалномаи пурра барои машқи саҳифаи 13 аз китоби математикаи синфи 5! Дар ин видео, мо ҷамъ ва тарҳи ададҳои мураккабро бо шарҳи оддӣ ва фаҳмо меомӯзем. Ба мо ҳамроҳ шавед, то ки дарсҳоро ба осонӣ фаҳмед ва ба саволҳоятон ҷавоб гиред. Ин таҳрири нав бо мисолҳои ҷолиб ва муносиб барои ҳама! Ҳамаи чизҳое, ки ба шумо лозим аст, дар ин ҷо аст.

Дар ин видео мо масъалахои саҳифаи 23 аз китоби математикаи синфи ҳафтумро ҳал мекунем. Ин видеои таълимии кӯмакрас ба донишҷӯён барои дарки беҳтари мавзӯъҳои математика мебошад. Агар хоҳед, ки дарси математикаи худро ба осонӣ фаҳмед, ин видеоро тамошо кунед.

Ба канали мо хуш омадед, ки дар он мо бо муҳаққиқи шинохта ва муаллими меҳрубон Амир Ҳоудӣ дар бораи математика суҳбат мекунем. Дарсҳои ҷолиб, фаҳмо ва шавқоварро дар ин ҷо пайдо мекунед, ки ба шумо дар фаҳмидани математика кӯмак мекунанд. Обуна шавед то ҳаргиз аз дарсҳои нави мо қафо намонед!

Дӯстони ҷон, дар ин видё дарси математика барои синфи 7-ро ба забони фаҳмо ва осон шарҳ медиҳем. Агар мехоҳӣ фаҳмишат зӯр шавад ва имтиҳонҳоро ба осонӣ супорӣ, ҳатман ин видёро тамошо кун! Саволҳо дорӣ? Дар коммент навис, ҳатман ҷавоб медиҳем. Подписка фаромӯш нашава!

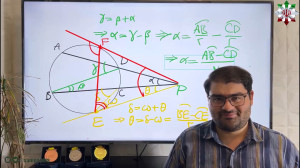
Марҳамат ба қисмати аввал аз силсилаи видеоҳо дар бораи доира ва кунҷ дар олимпиадаи математика! Дар ин видео, мо ба шумо нишон медиҳем, ки чӣ тавр масоили душворро дар бораи доира ва кунҷ осон ҳал кунед. Агар шумо ба олимпиадаи математика меҳрубон бошед ва мехоҳед, ки дар имтиҳонҳо ғолиб шавед, ин видео барои шумост! Ҳар як фаҳмиш ва саволҳои худатонро дар шарҳҳо гузоред!

Дар ин видео, мо ба қисми аввали дарси сеюми математика барои синфи ҳаштум назар мекунем. Бо мо бошед, то ба осонӣ фаҳмед ва дарсҳоро бо роҳҳои нав омӯзед. Агар дар ҷустуҷӯи роҳҳои осонтар барои фаҳмидани математика ҳастед, ин видео барои шумост! Аз ин фурсат истифода баред ва дарсҳоро аз худ кунед.

Мехоҳед дар олимпиадаи математика ғолиб шавед? Дар ин видео, мо ба шумо нишон медиҳем, ки чӣ тавр қуввати математика дар олимпиадаҳоро истифода бурдан мумкин аст. Қисми аввал аз силсилаи видеои мо барои омодагӣ ба олимпиадаҳои математика бо шумо ҳастем. Баъзе сирҳои муҳими ҳисобу китоб, ки метавонанд ба шумо кӯмак кунанд, то дар олимпиадаҳо муваффақ шавед. Омодагӣ бинед ва бо мо омӯзед!

Дар ин видео, мо бо муаллими математика дар бораи ҳаракатшиносӣ суҳбат мекунем. Барои фаҳмидани қоидаҳои асосии ҳаракат ва чӣ тавр онҳоро дар ҳаёти ҳаррӯза истифода кардан, ин видеоро тамошо кунед. Шумо омӯхтан мехоҳед, ки чӣ гуна математика метавонад дарк кардани ҳаракатро осон кунад? Биёед бо ҳам омӯзишро оғоз кунем!

Бачоҳо, дар ин видео Устод Ализода Хончаезор дарси дуюми математика барои синфи ёздаҳумро бо шумо тақвият медиҳад. Агар мехоҳед дар математика маҳорататонро боло баред, ин дарсро аз даст надиҳед! Дигар вақтҳои худро беҳуда сарф накунед, омадед даҳонатонро бо математика пур кунед!

Дар ин видео мо ба дараҷаи панҷуми синфи ҳамаҷонибаи математикаи синфи 11 меравем. Шуъбаи таҷрибӣ ва математика барои шогирдони фаъол ва доно омода шудааст. Ҳамаи масъалаҳои муҳим ва мафҳумҳои асосиро дар ин дарс меомӯзем. Агар мехоҳед ба донишҳои худ дар математика такя кунед, ин видеоро аз даст надиҳед!

Дар ин видео, мо ба шумо бо роҳҳои осон ва шавқовар математика омӯзиш медиҳем. Агар шумо ҳамеша фикр мекардед, ки математика мушкил аст, пас ин видео барои шумост! Бо мо ҳамроҳ шавед ва ба ҷаҳони ҷолиби математика ғарқ шавед!

Ҳалномаи саҳифаи 69 китоби риёзи барои онҳое, ки мехоҳанд дарсҳои риёзиро беҳтар фаҳманд. Дар ин видео, масъалаҳои саҳифаи 69-ро бо тарзи осон ва фаҳмо ҳал мекунем. Бо мо ҳамроҳ шавед, то дар риёзи устувор шавед!

Эшлиро ёфтем, аммо ҳодисаи ғайричашмдошт ба вуқӯъ пайваст! Чархбол ба нестӣ рафт ва акнун мо дар ин қисми ҷолибтарини бозии Resident Evil 4 бо хатарҳои нав рӯ ба рӯ мешавем. Инҷо ҳама чизро хоҳед дид: аз муомилаҳои сахт то муқовиматҳои шадид. Ҳалномаи навбатии Леонро бинед ва ба ҳар як қадамаш ҳамроҳ шавед!